This page discusses the analysis and also shows how the analyses were done using the R computer package. For more details on using R, consult the very short tutorial or the more complete tutorial.
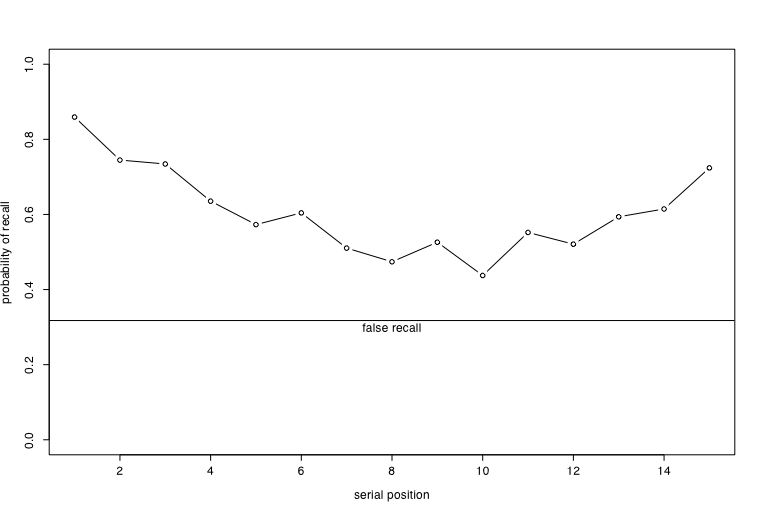
Before examining the recognition of true and false memories, we examined the effect of several variables upon the probability of recalling a true word. The first analysis is merely descriptive. Does recall show the normal serial position effect? How does the probability of false recall compare to the probability of real recall?
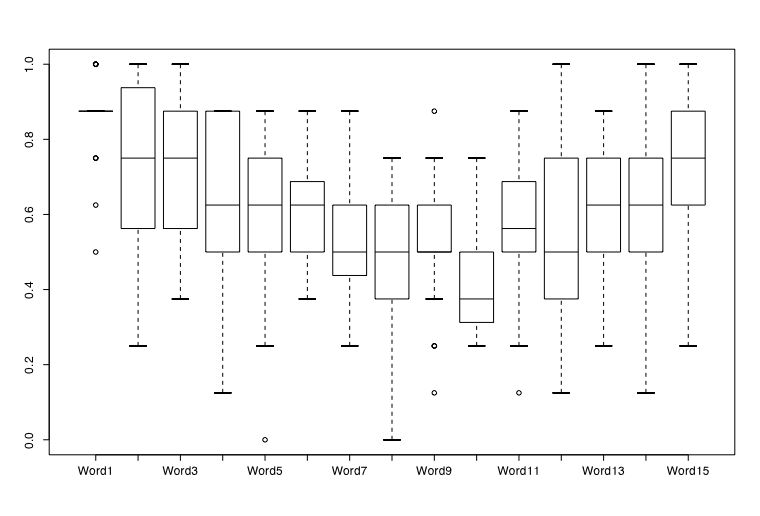
The data were transferred from the scoring sheets into a spreadsheet. These data were then read into R by using the read.clipboard() function. Two descriptive graphs were made: a boxplot of the 15 words which shows the variability of the subjects' data, as well as a more conventional plot of the means.
The raw data Word1 Word2 Word3 Word4 Word5 Word6 Word7 Word8 Word9 Word10 Word11 Word12 Word13 Word14 Word15 8 7 8 4 7 5 4 3 4 4 5 3 4 4 6 7 6 7 4 6 5 4 3 4 4 5 7 5 4 7 7 6 8 5 6 5 5 6 6 3 5 6 6 7 7 7 5 6 6 6 7 4 4 5 5 6 5 5 3 5 8 7 8 6 3 6 2 4 4 3 2 1 2 7 8 7 8 5 4 6 4 3 3 5 4 6 3 6 6 5 8 8 5 5 2 7 5 4 4 6 4 3 6 6 5 8 2 4 1 4 3 3 3 5 3 4 1 6 3 7 7 6 7 5 5 4 5 5 4 4 2 5 5 5 5 6 5 4 6 5 5 3 4 2 2 2 3 3 5 6 7 8 7 7 6 3 4 5 6 3 5 7 5 5 3 6 4 5 2 3 5 4 0 2 3 4 3 4 6 5 8 8 7 7 4 5 4 3 7 2 7 4 6 6 6 5 4 5 3 0 6 5 3 2 2 4 5 5 4 8 7 6 5 4 4 3 4 5 5 5 5 4 7 5 7 7 4 4 7 4 5 4 4 3 4 4 6 5 6 8 7 8 7 7 5 5 4 4 6 5 6 5 5 6 4 7 8 6 7 7 3 4 5 4 4 1 6 3 4 4 7 7 7 7 4 6 4 3 5 6 5 6 6 4 5 7 4 7 7 3 6 7 6 4 2 6 8 7 8 6 6 5 3 3 4 5 3 4 1 2 4 3 2 1 2 7 7 8 6 5 4 5 5 4 2 6 2 5 6 6 4 3 4 4 6 4 3 2 4 3 4 2 2 3 7 7 7 4 5 5 5 5 3 5 3 4 2 4 4 7To just copy these data into R, we can read from the clipboard. Unfortunately, until version 2.1.0 comes out, this command is different for PCs and Macs. But to get around this, I have created the "read.clipboard()" function. This may be obtained from the web by using the source command:
source("http://personality-project.org/r/useful.r") #useful additions to r
#now copy the data into the clipboard and read the clipboard
recall.words <- read.clipboard() #reads the data
recall.words <- recall.words/8 #convert to probabilities of recall
recall.words #echos the data to the console
boxplot(recall.words) #a boxplot of the results
plot(recall.words,type="b",ylim=c(0,1),xlab = "serial position", ylab ="probability of recall")
abline(h=2.54/8) #a horizontal line for the false recalls
text(8,.3,"false recall") #add a label to the graph
results in the boxplot and the more conventional graphic


These two graphs suggest that normal memory processes were involved while subjects were learning the 16 lists. Words at the beginning and end of each list were much more likely to be recalled than were words in the middle of the list. False memories were recalled about 32% of the time.
To do this required entering the data into a data sheet and then reading it into the R system.
The first data set to read is the recall data for a few specific locations (1, 8 and 10) on each list. The variable labels reflect the condition of 2 or 3 seconds of study time and 45 or 90 seconds of recall time. Not in R, I combined the two replications for each subject for each condition.
r24 r34 r29 r39 3 4 5 4 2 5 5 4 3 4 4 3 4 5 5 2 2 4 5 5 2 2 1 3 2 3 4 5 3 6 3 3 3 4 4 3 2 3 4 2 4 3 2 5 4 3 5 4 3 4 3 4 3 3 4 4 4 5 4 5 4 3 1 3 4 2 3 5 3 0 3 5 4 4 4 4 3 4 3 6 1 3 4 6 3 5 4 3 2 2 4 3
#now copy the data into the clipboard and read the clipboard
recall <- read.clipboard() #reads the data recall #echos the data to the console #produces this output recall r24 r34 r29 r39 1 3 4 5 4 2 2 5 5 4 ... 21 1 3 4 6 22 3 5 4 3 23 2 2 4 3
These are the number of words recalled (6 maximum) in the 2 second or 3 second study trials and the 45 or 90 second recall trials. To convert these raw numbers to probability of recall, we can divide them all by 6.
recall <- recall/6 #the numbers now range from 0 to 1 to reflect the probability of recall.
We can examine whether there is an effect or study and recall interval by doing an analysis of variance. This allows us to ask the inferential question about how much of the variance of the Dependent Variable is associated with our manipulations of the Independent Variables. We ask the question of how likely is it to observe this much variation due to the IVs if there is in fact no effect of the IVs in the population. We are interested in the means for our conditions as well as the variance between means compared to the variance within subjects.
The analysis we will do is a complete within subject analysis which requires some manipulation of the data to put it into a form for an anova. ANOVA is done as a linear model (regression) of the IVs against the DV. With repeated measures, subjects becomes a variable and we string out the 23 * 4 array into a single vector of 92 values. We use the stack function to do this. Then we add values for the IVs, including the subject as an IV. We put the entire set into a "dataframe".
(Believe it or not, this is actually simpler than it seems at first glance. The dataframe can be thought of as a number of rows and columns where we need to define what goes into each column. Column 1 is simply the data for each subject, strung out into 1 long column. Column 2 gives us the variable names from the original data. Column 3 (study) is either "short" or "long". It is made up by repeating the names "short" and "long" numcases (23) times each. Because this does not fill up the column, this pattern is then repeated until it does. Column 4 (time) does the same thing but puts in "45" or "90" 2 * numcases times each. It also doesn't fill up the column and so automatically repeats until it does. Finally, the last column gives labels to each subject. These labels are then repeated 4 times.)
#set a few general variables
numcases <- 23 #how many subjects
numlevelsvar1 <- 2 #how many levels of variable 1?
numlevelsvar2 <- 2 #how many levels of variable 2?
numvar <- numlevelsvar1 * numlevelsvar2 #figure out the number of variables
stackeddata <- stack(recall) #strings out the data into 1 column
#create a dataframe with the DVs followed by the IVs
data.df <- data.frame(stackeddata,
study = factor(rep(c("short","long"),c(numcases,numcases))),
time = factor(rep(c("45","90"),c(numlevels1*numcases,numlevels1*numcases))),
subj = factor(rep(paste("subj",1:numcases, sep=""), numvar))
)
The original data were
recall
r24 r34 r29 r39
1 0.50 0.67 0.83 0.67
2 0.33 0.83 0.83 0.67
...
22 0.50 0.83 0.67 0.50
23 0.33 0.33 0.67 0.50
The "stacked" data with the variable values added are
values ind study time subj
1 0.5000000 r24 short 45 subj1
2 0.3333333 r24 short 45 subj2
...
22 0.5000000 r24 short 45 subj22
23 0.3333333 r24 short 45 subj23
24 0.6666667 r34 long 45 subj1
...
46 0.3333333 r34 long 45 subj23
47 0.8333333 r29 short 90 subj1
...
69 0.6666667 r29 short 90 subj23
70 0.6666667 r39 long 90 subj1
71 0.6666667 r39 long 90 subj2
...
91 0.5000000 r39 long 90 subj22
92 0.5000000 r39 long 90 subj23
Now that the data are in a useful form, we do the Analysis of Variance (ANOVA) with repeated measures.
recall.aov= aov(values ~ time * study + Error(subj/(time * study)), data=data.df) #do the ANOVA
print(model.tables(recall.aov,"means"),digits=3) #show the cell means for the anova table
summary(recall.aov) #show the output for ANOVA
Produces this output:
recall.aov= aov(values ~ time * study + Error(subj/(time * study)), data=data.df) #do the ANOVA
print(model.tables(recall.aov,"means"),digits=3) #show the cell means for the anova table
Tables of means
Grand mean
0.5869565 <- overall probability of recall
time
45 90
0.54 0.634 <- it seems as if more words were recalled in 90 than 45 seconds
rep 46.00 46.000
study
long short
0.623 0.551 <- and that longer study times helped later recall
rep 46.000 46.000
time:study
study
time long short
45 0.59 0.49
rep 23.00 23.00
90 0.66 0.61
rep 23.00 23.00
>
#now test these differences for statistical significance
#that is, how likely would you observe these differences if the population means were identical?
> summary(recall.aov) #show the output
Error: subj
Df Sum Sq Mean Sq F value Pr(>F) <- the within subject error term
Residuals 22 0.81824 0.03719
Error: subj:time
Df Sum Sq Mean Sq F value Pr(>F)
time 1 0.20411 0.20411 5.3612 0.0303 * <- the effect of recall time has a "p value " of .03
Residuals 22 0.83756 0.03807
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Error: subj:study
Df Sum Sq Mean Sq F value Pr(>F)
study 1 0.12077 0.12077 5.9219 0.02353 * <- the effect of study time has a "p value" of .02
Residuals 22 0.44867 0.02039
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Error: subj:time:study
Df Sum Sq Mean Sq F value Pr(>F)
time:study 1 0.01087 0.01087 0.232 0.6348
Residuals 22 1.03080 0.04685
Here are all the commands grouped together:
source("http://personality-project.org/r/useful.r") #get some useful additions
#now copy the data into the clipboard and read the clipboard
recall <- read.clipboard() #reads the data
recall #echos the data
recall <- recall/6 #convert to probability of recall
#set a few general variables
numcases <- 23 #how many subjects
numlevelsvar1 <- 2 #how many levels of variable 1?
numlevelsvar2 <- 2 #how many levels of variable 2?
numvar <- numlevelsvar1 * numlevelsvar2
stackeddata <- stack(recall) #strings out the data into 1 column
#create a dataframe with the DVs followed by the IVs
data.df <- data.frame(stackeddata,
study = factor(rep(c("short","long"),c(numcases,numcases))),
time = factor(rep(c("45","90"),c(numlevels1*numcases,numlevels1*numcases))),
subj = factor(rep(paste("subj",1:numcases, sep=""), numvar))
)
recall.aov= aov(values ~ time * study + Error(subj/(time * study)), data=data.df) #do the ANOVA
print(model.tables(recall.aov,"means"),digits=3) #show the cell means for the anova table
summary(recall.aov) #show the output for ANOVA
More than just examining recall, we were interested in the effect of our manipulations on recognition of words that were presented (True memories) and high associate words that were not presented (False memories). In addition, we were interested in whether recognition for True and False memories are affected by study time (2 vs 3 seconds) and recall interval (45 vs. 90). We were also interested in whether having a chance to recall (Math vs. Recall) makes a difference. This is a complicated analysis and we will build up to it by doing a number of simpler analyses first. In fact, the ANOVA was developed for just this case. It allows us to examine many effects at the same time, from broad main effects to complex interactions between variables.
The raw data are the number of words correctly and incorrectly recognized on the recognition sheet depending upon conditions. The variable labels are an attempt at specifying conditions (e.g., r vs f for real versus false, 0 or 1 for no recall (math) vs recall, 2 vs 3 for 2 versus 3 seconds of study, and 4 vs 9 for 45 versus 9 seconds recall interval).
Before doing any analyses, we will need to rescale the numbers to put them on a 0 - 1 scale. The reall numbers range from 0-6 and the false from 0-2. We can do this by dividing the recognition matrix by a vector of 6s and 2s. Then we need to stack the data and create a data frame with the appropriate conditions.
r024 r029 r034 r039 r124 r129 r134 r139 f024 f029 f034 f039 f124 f129 f134 f139
1 5 4 6 4 4 6 6 5 1 1 2 2 1 0 1 2
2 5 5 3 4 5 5 6 5 0 0 1 0 1 1 0 0
3 5 1 4 6 6 6 6 4 0 0 0 1 1 1 0 0
4 6 3 6 3 4 5 5 3 1 2 2 1 2 1 2 0
5 6 0 5 5 3 4 5 5 1 1 2 0 1 1 0 0
6 0 0 1 3 3 3 3 4 0 0 1 1 1 2 1 2
7 5 4 6 5 3 5 5 5 1 2 2 1 2 1 1 2
8 5 4 4 5 5 5 6 3 0 0 0 0 1 0 1 1
9 3 3 5 4 5 5 6 5 0 0 0 0 1 1 0 0
10 5 2 4 6 3 5 5 3 1 2 2 2 2 2 2 1
11 2 5 6 6 5 3 6 6 1 1 1 0 0 1 1 1
12 3 3 6 1 5 4 6 6 0 0 0 0 1 2 1 1
13 5 5 4 5 4 4 5 5 2 1 1 1 0 0 1 1
14 5 6 5 5 5 6 6 6 1 0 1 1 1 1 1 2
15 6 5 6 4 6 5 6 6 2 1 1 0 0 0 1 0
16 3 6 6 3 6 2 6 4 0 0 1 1 0 1 0 1
17 6 5 6 4 5 6 5 4 2 0 2 1 1 1 2 1
18 3 5 6 4 6 5 3 5 1 2 2 1 1 2 1 2
19 5 6 6 4 6 6 6 6 2 0 1 1 1 1 0 1
20 1 0 0 0 2 2 5 5 1 1 1 1 2 0 0 1
21 2 3 6 2 3 6 4 6 1 0 2 1 1 2 2 2
22 5 6 6 4 6 5 6 4 2 1 2 2 1 1 1 0
23 2 5 3 4 1 5 4 4 0 0 0 0 1 1 1 0
#Copy these to the clipboard and then read the clipboard:
recognition <- read.clipboard()
recognition[,1:8] <- recognition[,1:8]/6 #divide the first 8 by 6, the last 8 by 2
recognition[9:16]<-recognition[,9:16]/2
#set a few general variables
numcases <- 23 #how many subjects
numlevelsvar1 <- 2 #how many levels of variable 1?
numlevelsvar2 <- 2 #how many levels of variable 2?
numlevelsvar3 <- 2 #how many levels of variable 3?
numlevelsvar4 <- 2 #how many levels of variable 4?
numvar <- numlevelsvar1 * numlevelsvar2 * numlevelsvar3 * numlevelsvar4
stackeddata <- stack(recognition) # string out into a 16*23 long vector
#create a dataframe with the DVs followed by the IVs
data.df <- data.frame(stackeddata,
wordtype = factor(rep(c("real","false"),c(numvar*numcases/2,numvar*numcases/2))),
recall = factor(rep(c("math","recall"),c(numcases*numlevels1*numlevels2,numcases*numlevels1*numlevels2))),
study = factor(rep(c("short","long"),c(numcases*numlevels1,numcases*numlevels1))),
time = factor(rep(c("45","90"),c(numcases,numcases))),
subj = factor(rep(paste("subj",1:numcases, sep=""), numvar))
)
recog.aov= aov(values ~ wordtype* recall* time * study + Error(subj/(wordtype*recall*time * study)), data=data.df) #do the ANOVA
print(model.tables(recog.aov,"means"),digits=3) #show the cell means for the anova table
summary(recog.aov) #show the output for ANOVA
This produces pages of output, first of the means, organized by the various combinations of the independent variables, and then the actual inferential tests using ANOVA.
Tables of means
Grand mean What is the overall mean probability of recognition?
0.5978261
wordtype Real words are recognized more than false words
false real
0.454 0.742
rep 184.000 184.000 rep (or replications) is how many observations went into this mean
recall more words were recognized if given a chance to recall
math recall
0.562 0.634
rep 184.000 184.000
time more words were recognized after a shorter recall interval!
45 90
0.63 0.566
rep 184.00 184.000
study longer times (3 seconds vs. 2 secs) lead to better recognition
long short
0.624 0.572
rep 184.000 184.000
wordtype:recall
recall
wordtype math recall
false 0.4 0.5
rep 92.0 92.0
real 0.7 0.8
rep 92.0 92.0
wordtype:time
time
wordtype 45 90
false 0.5 0.4
rep 92.0 92.0
real 0.8 0.7
rep 92.0 92.0
recall:time longer time doing math seemed to reduce later recognition
time
recall 45 90
math 0.6 0.5
rep 92.0 92.0
recall 0.6 0.6
rep 92.0 92.0
wordtype:study
study
wordtype long short
false 0.5 0.4
rep 92.0 92.0
real 0.8 0.7
rep 92.0 92.0
recall:study
study
recall long short
math 0.6 0.5
rep 92.0 92.0
recall 0.6 0.6
rep 92.0 92.0
time:study
study
time long short
45 0.7 0.6
rep 92.0 92.0
90 0.6 0.6
rep 92.0 92.0
wordtype:recall:time
, , time = 45
recall
wordtype math recall
false 0.5 0.5
rep 46.0 46.0
real 0.7 0.8
rep 46.0 46.0
, , time = 90
recall
wordtype math recall
false 0.4 0.5
rep 46.0 46.0
real 0.6 0.8
rep 46.0 46.0
wordtype:recall:study
, , study = long
recall
wordtype math recall
false 0.5 0.4
rep 46.0 46.0
real 0.7 0.8
rep 46.0 46.0
, , study = short
recall
wordtype math recall
false 0.4 0.5
rep 46.0 46.0
real 0.6 0.8
rep 46.0 46.0
wordtype:time:study
, , study = long
time
wordtype 45 90
false 0.5 0.4
rep 46.0 46.0
real 0.8 0.7
rep 46.0 46.0
, , study = short
time
wordtype 45 90
false 0.5 0.4
rep 46.0 46.0
real 0.7 0.7
rep 46.0 46.0
recall:time:study
, , study = long
time
recall 45 90
math 0.7 0.5
rep 46.0 46.0
recall 0.7 0.6
rep 46.0 46.0
, , study = short
time
recall 45 90
math 0.6 0.5
rep 46.0 46.0
recall 0.6 0.6
rep 46.0 46.0
wordtype:recall:time:study
, , time = 45, study = long
recall
wordtype math recall
false 0.59 0.43
rep 23.00 23.00
real 0.80 0.88
rep 23.00 23.00
, , time = 90, study = long
recall
wordtype math recall
false 0.39 0.46
rep 23.00 23.00
real 0.66 0.79
rep 23.00 23.00
, , time = 45, study = short
recall
wordtype math recall
false 0.43 0.50
rep 23.00 23.00
real 0.67 0.73
rep 23.00 23.00
, , time = 90, study = short
recall
wordtype math recall
false 0.33 0.50
rep 23.00 23.00
real 0.62 0.78
rep 23.00 23.00
After all of these means, we want to think about which make the most difference. That is to say, some of these differences are what we would expect by chance. Lets look at the ANOVA output to see which means are most important to think about. Each ANOVA table reports a number of different things.
Analysis of Variance summary table:
Error: subj
Df Sum Sq Mean Sq F value Pr(>F)
Residuals 22 6.3741 0.2897
Error: subj:wordtype
Df Sum Sq Mean Sq F value Pr(>F)
wordtype 1 7.6332 7.6332 27.268 3.084e-05 ***
Residuals 22 6.1585 0.2799
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Error: subj:recall
Df Sum Sq Mean Sq F value Pr(>F)
recall 1 0.4831 0.4831 3.2326 0.08592 .
Residuals 22 3.2877 0.1494
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Error: subj:time
Df Sum Sq Mean Sq F value Pr(>F)
time 1 0.36987 0.36987 5.1003 0.03418 *
Residuals 22 1.59541 0.07252
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Error: subj:study
Df Sum Sq Mean Sq F value Pr(>F)
study 1 0.25393 0.25393 4.8921 0.03767 *
Residuals 22 1.14191 0.05190
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Error: subj:wordtype:recall
Df Sum Sq Mean Sq F value Pr(>F)
wordtype:recall 1 0.1090 0.1090 1.4993 0.2337
Residuals 22 1.5993 0.0727
Error: subj:wordtype:time
Df Sum Sq Mean Sq F value Pr(>F)
wordtype:time 1 0.00483 0.00483 0.0998 0.755
Residuals 22 1.06461 0.04839
Error: subj:recall:time
Df Sum Sq Mean Sq F value Pr(>F)
recall:time 1 0.32880 0.32880 5.379 0.03006 *
Residuals 22 1.34481 0.06113
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Error: subj:wordtype:study
Df Sum Sq Mean Sq F value Pr(>F)
wordtype:study 1 0.05918 0.05918 0.9305 0.3452
Residuals 22 1.39915 0.06360
Error: subj:recall:study
Df Sum Sq Mean Sq F value Pr(>F)
recall:study 1 0.15972 0.15972 2.3211 0.1419
Residuals 22 1.51389 0.06881
Error: subj:time:study
Df Sum Sq Mean Sq F value Pr(>F)
time:study 1 0.12077 0.12077 2.1542 0.1563
Residuals 22 1.23339 0.05606
Error: subj:wordtype:recall:time
Df Sum Sq Mean Sq F value Pr(>F)
wordtype:recall:time 1 0.04348 0.04348 0.7037 0.4106
Residuals 22 1.35930 0.06179
Error: subj:wordtype:recall:study
Df Sum Sq Mean Sq F value Pr(>F)
wordtype:recall:study 1 0.14614 0.14614 3.0668 0.09384 .
Residuals 22 1.04831 0.04765
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Error: subj:wordtype:time:study
Df Sum Sq Mean Sq F value Pr(>F)
wordtype:time:study 1 0.03653 0.03653 0.6404 0.4321
Residuals 22 1.25513 0.05705
Error: subj:recall:time:study
Df Sum Sq Mean Sq F value Pr(>F)
recall:time:study 1 0.00483 0.00483 0.0804 0.7794
Residuals 22 1.32156 0.06007
Error: subj:wordtype:recall:time:study
Df Sum Sq Mean Sq F value Pr(>F)
wordtype:recall:time:study 1 0.03653 0.03653 0.4152 0.526
Residuals 22 1.93569 0.08799
From the ANOVA table we can see that there are 3 main effects and one interaction that are worth discussing: Word type (real or false), recall time (45 vs. 90) and study time (2 vs 3). In addition, recall vs. math interacted with recall time. Note that real versus false did not interact with anything, suggesting that the process of retrieving "real" memories and "false" memories do not differ.